Attività specifica e concentrazione del radon nel tempo in uno spazio confinato. Studi analitici e grafici di una serie di casi specifici.
Per una maggior comprensione delle grandezze fisiche e chimiche citate e sui loro valori vedi: “Unità di misura delle grandezze del Rn-222 e dei suoi figli“.

La funzione concentrazione specifica di un elemento (ad esempio azoto o radon) nel volume “m” di uno spazio confinato (definito come spazio delimitato da confini, a loro volta esclusi), isolato o no (nel senso che non ha, oppure ha, scambi con l’esterno), espressa in nuclidi al metro cubo, che d’ora in poi chiameremo C(t,x,y,z) [Nucl./m3], dipende, oltre che dalle condizioni al tempo zero, dalle caratteristiche della loro sorgente P(t,x,y,z) [Nucl./(m3sec)], la produzione, e da quelle della loro sottrazione Q(t,x,y,z) [Nucl./(m3sec)].
P e Q sono quindi produzione e sottrazione specifica di nuclidi nell’unità di tempo nel volume “m”. Se lo spazio è isolato verso l’esterno, produzione e sottrazione sono necessariamente interne al volume, altrimenti si ha un flusso di massa in entrata o uscita. P può consistere nella trasmutazione di un eventuale radionuclide genitore o nel flusso di massa in entrata. Q invece può essere dovuta a decadimento, se l’elemento in osservazione è radioattivo, o a flusso di massa in uscita. Ipotizziamo dunque inesistente la produzione o la diminuzione dell’elemento per altre cause.
Per flusso di massa intendiamo un incremento o una sottrazione specifica di radionuclidi di quell’elemento verso il o dal volume confinato, se non isolato, intendendo i confini stessi, ove tra l’altro si potrebbe depositare il “plate-out”, come non facenti parte di esso. Importante tener presente infine che la sottrazione Q di un radionuclide è legata (proporzionalmente o meno) alla sua concentrazione istantanea.
Ipotizzando che, come normalmente avviene, C, P e Q non dipendano dalle coordinate spaziali si ha allora:
dC(t) / dt = P(t) – Q(t)
Caso 1 – Nuclide con produzione costante e sottrazione nulla.
Studiamo il caso di uno spazio confinato “m”, isolato, con C(t) e P(t) non dipendenti dalle coordinate spaziali cioè spazialmente uniformi e Q=0. Inoltre P sia costante nel tempo, quindi P=costante=F [Nucl./(m3sec)].
L’andamento di C(t) [Nucl./m3] nel tempo, da una situazione iniziale C(0)=0, è quindi:
C(t) = F*t
Se per lo spazio confinato “m” prendiamo la biosfera del nostro pianeta, questo può essere per esempio il caso di un elemento stabile A (l’ N-14) figlio (per decadimento beta) di un elemento radioattivo B (il C-14). Quest’ultimo è prodotto principalmente dall’impatto sull’atmosfera di neutroni cosmici, con una produzione limitata ma costante e un tempo di dimezzamento sufficientemente grande (T1/2 = 5700 [anni]; λB = 3,856 E -12 [sec-1]). Possiamo perciò considerare la sua concentrazione in natura CB costante. Dunque si ha una sorgente di A dovuta al decadimento radioattivo del genitore B con P=λBCB e una concentrazione:
CA(t) = λB*CB*t
Si tratta di un andamento rettilineo con coefficiente angolare pari a λBCB. Quest’ultimo indica la crescita della concentrazione, che è tanto più rapida quanto maggiori sono la costante di decadimento e la concentrazione di B. Se non intervengono fenomeni che rendono Q diversa da zero, la crescita è teoricamente infinita.
Nel caso che C(0) sia diverso da zero il grafico inizierà da quel valore.
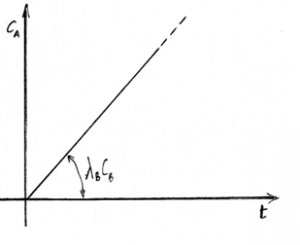
Ovviamente la funzione P può derivare da altra e diversa causa, come ad esempio, se “m” non fosse isolato, da un flusso specifico di massa F [Nucl./(m3sec)] del nuclide A proveniente dall’esterno. Se F è costante nel tempo si ha di nuovo:
CA(t) = F*t
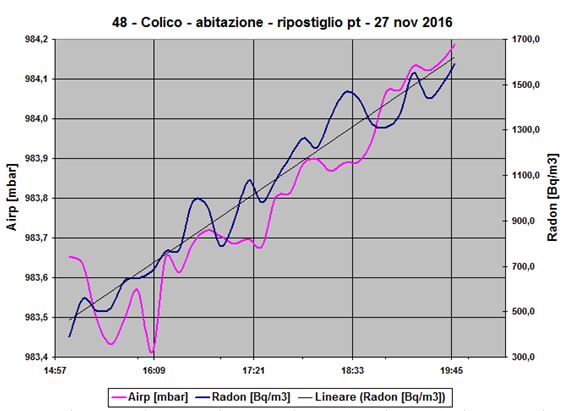
Prendiamo un altro esempio, stavolta rilevato strumentalmente: il grafico n. 48. Qui A è un elemento radioattivo, il Rn-222, e “m” è ancora non isolato verso il terreno sottostante.
La concentrazione C(t) [Nucl./m3] di radionuclidi di A è sostituita, per facilità d’uso, dall’attività A(t) = C(t) * λA [Bq/m3] che gli è proporzionale. E’ un caso reale di accumulo nel tempo del Rn-222 in uno spazio confinato, non isolato dal terreno. Il valore iniziale A(0) è pari a 400 [Bq/m3]. Il grafico inizia al momento della chiusura del locale, quando il valore del flusso di massa in uscita diventa pari a zero, mentre P, la sorgente di radon dal terreno, è approssimativamente un flusso costante (P = F = 4,242E+04 [Nucl./(m3sec)]. Si può considerare Q=0 in quanto che, oltre alla mancanza di flussi di massa in uscita, nelle poche ore di rilievo del grafico, il radon non ha tempo di decadere sensibilmente. Nel grafico si notano, invece, oscillazioni intorno alla linea di tendenza causate dalla non costanza di P e da fattori sperimentali. La pressione atmosferica cresce di meno di un mbar in circa quattro ore e quindi ha poco impatto.
Caso 2 – Radionuclide con produzione e coefficiente totale di sottrazione costanti.
Studiamo adesso il caso di un elemento A radioattivo in cui P è costante nel tempo, ma Q diversa da 0. Il locale confinato “m” non è isolato. Torniamo all’esempio del grafico sperimentale n. 48, adesso ampliato, quando, al passare del tempo, si inizia a rilevare la presenza anche di altri fenomeni. Si ha ancora l’entrata di A dal terreno nel locale confinato (ancora P = costante = F), ma si hanno adesso anche flussi specifici di massa (radionuclidi di A al metro cubo al secondo) verso l’esterno che rendono Q diversa da zero. Questi flussi potrebbero essere dovuti a fenomeni di “plate-out” (utilizziamo per definirli una λpl ) e/o di ventilazione (con una costante λV , che è positiva se il flusso di massa esce). Inoltre contribuisce a Q anche il decadimento radioattivo (con costante di decadimento λA).
Quindi si ha il seguente equilibrio:
dCA / dt = P(t) – Q(t) = F – λA*CA – λpl*CA – λV*CA = F – λtot *CA
Abbiamo chiamato λtot [sec-1] = λA – λpl – λV coefficiente totale di sottrazione. E’ la funzione che lega Q(t) a CA(t), come abbiamo accennato all’inizio.
Ovviamente λA [sec-1] è costante nel tempo, ma λV [sec-1] e λpl [sec-1] generalmente no. Pertanto CA [Nucl./m3] è spesso una funzione variabile, anche non linearmente, del tempo.
Nella realtà il fenomeno può essere esemplificato sempre dal grafico precedente, dove A è il Rn-222, adesso esteso nel tempo:
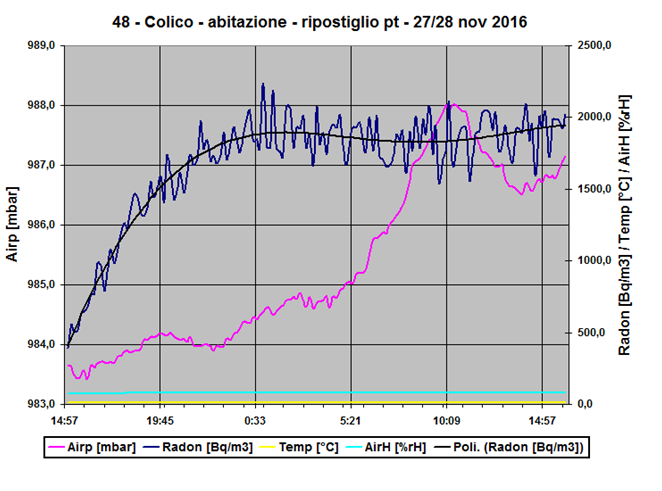
Nel grafico la ventilazione e il decadimento radioattivo del Rn-222, in sintesi Q, non fanno quasi sentire i loro effetti nelle prime ore. Ma dopo circa 10 ore hanno addirittura compensato P tanto da portare la concentrazione specifica CA ad un valore di equilibrio (la corrispondente attività specifica AA è circa 1875 [Bq/m3]). La linea di tendenza polinomiale ne approssima i valori molto chiaramente. Le oscillazioni del valore del radon intorno alla linea di tendenza sono la conseguenza del fatto che, oltre alla non costanza di P (si possono persino avere degli sbuffi di radon in entrata dal terreno o delle pause), anche λV è variabile nel tempo per causa di una molteplicità di fattori.
Vediamo invece, teoricamente, che cosa si ottiene.
Ipotizziamo che λpl e λV siano costanti e chiamiamo λpl + λV = λrem coefficiente di “removal”. Il valore totale del coefficiente totale di sottrazione é allora:
λtot = λA + λpl + λV = λA + λrem
E quindi risolvendo possiamo riscrivere (con F e λtot costanti):
CA(t) = CA(0) exp (- λtot*t) + F/λtot [1 – exp (- λtot*t)]
Che dunque è il caso generale dell’andamento della concentrazione del Rn-222, CA(t), nell’ambiente confinato, se λtot e F sono costanti.
Consideriamo adesso una esemplificazione del caso generale con le seguenti assunzioni:
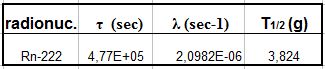
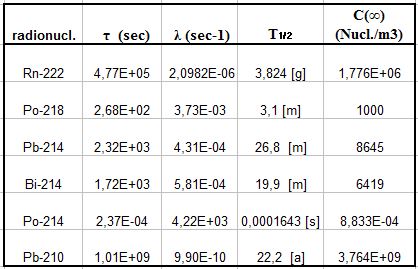
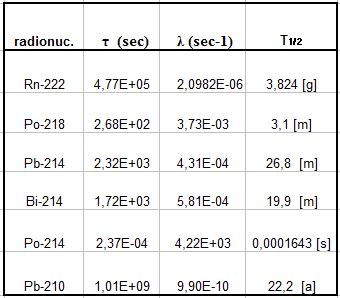
A = Rn-222; CA(0) = 0 [Nucl./m3]; F = 4,2426E+04 [Nucl./(m3sec)]; λrem= 0; λtot= λA= λRn= 2,0982E-6 [sec-1];
Si ha:
CRn(t) [Nucl./m3] = 2,022E+10 [1 – exp (- λRn*t) ]
Ricordando adesso la grandezza ARn(t) [Bq/m3], che è la corrispondente attività specifica, si ha:
ARn(t) [Bq/m3] = λRn * CRn(t) [Nucl./m3] = 4,2426E+4 (1- exp (- λRn *t))
da cui si ha:
CRn(∞) = 2,022E+10 [Nucl./m3] e ARn(∞) = 42’426 [Bq/m3]
Da notare che in termini di attività la produzione P = F * λRn = 0,08902 [Bq/(m3sec)]
Ricordando adesso che:
si possono costruire la tabella e il grafico corrispondenti, dove è plottata l’attività ARn(t) [Bq/m3]:
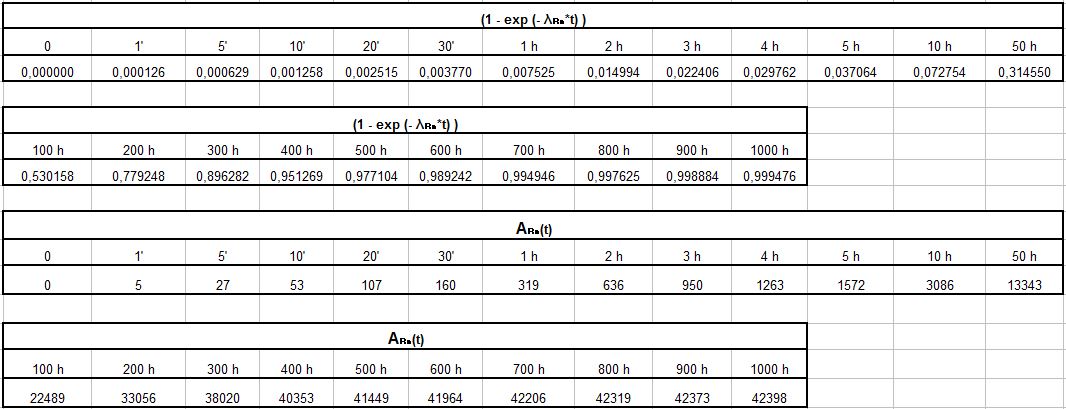
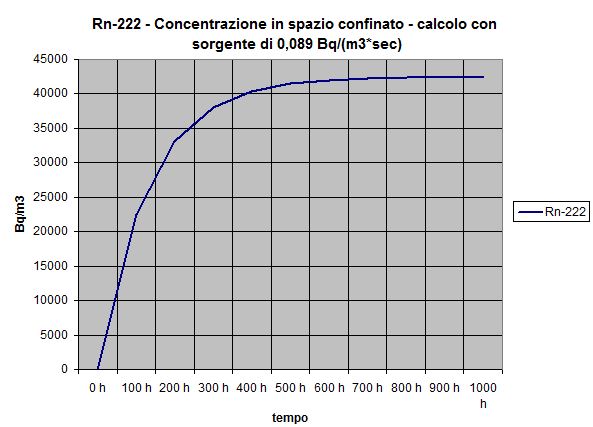
Si nota che, in mancanza di fenomeni di “removal” e un coefficiente di rimozione dovuto solamente al decadimento, e per causa di una sorgente forte, la concentrazione raggiunge un valore di equilibrio molto alto (F / λRn). L’equilibrio è raggiunto prima di un mese, ovvero, come noto, dopo circa sette T1/2. Confrontando con il grafico 48 sopra esaminato, si vede come lì la presenza delle ventilazioni (appunto i fenomeni di “removal”) riduca molto il livello di equilibrio raggiunto (attività specifica di circa 1875 [Bq/m3] invece di 42’426 [Bq/m3] e dopo solo 10 ore). Nelle prime cinque ore i due andamenti invece si sovrappongono quasi (vedi dati dalla tabella). Il grafico ottenuto teoricamente della figura 4 e quello sperimentale della figura 3 sono perfettamente coerenti tra loro.
Caso 3 – Radionuclide con produzione nulla e coefficiente totale di sottrazione costante.
Ipotizziamo adesso che la sorgente P del locale confinato di cui sopra, dopo il raggiungimento dell’equilibrio di 2,022E+10 [Nucl./m3] (corrispondente ad un’attività di 42’426 [Bq/m3]), si interrompa (F = 0). Utilizzando la formula precedente di CA(t) si ricava, per il Rn-222 e con λtot = λRn :
CRn(t) = CRn(0) exp (- λRn*t)
La concentrazione del Rn-222 diminuirà gradatamente a partire dal valore iniziale per la sola sottrazione dovuta al decadimento radioattivo (unica che può essere considerata costante) e il valore diviene praticamente nullo dopo circa sette T1/2.
Calcoliamo la tabella e costruiamo il grafico:
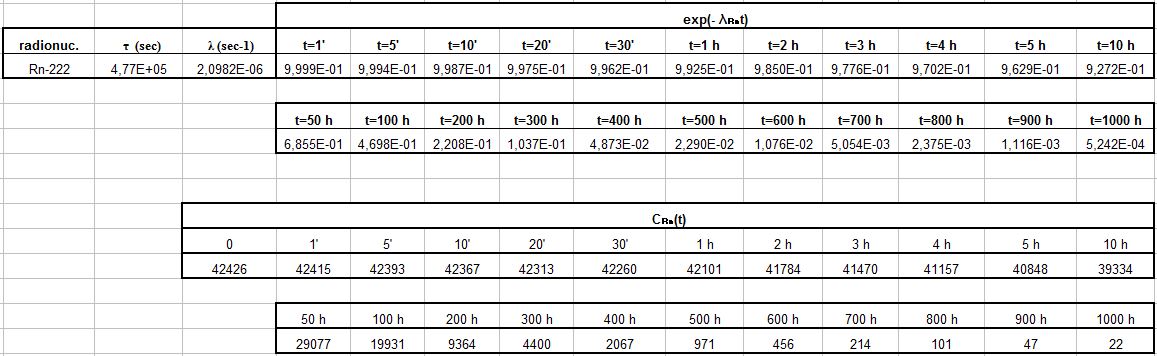
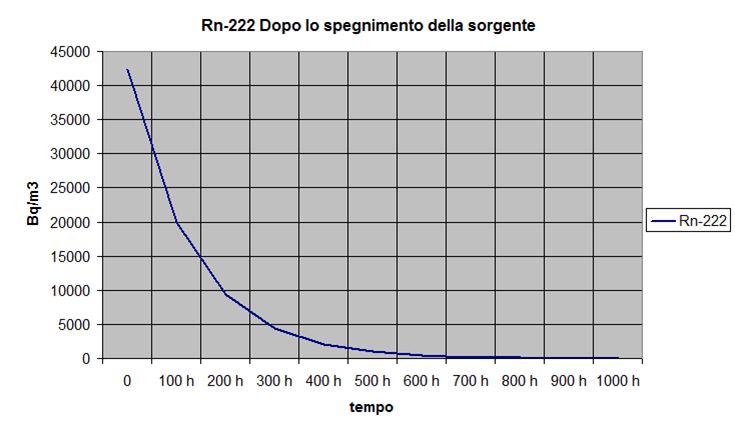
Caso 4 – Radionuclide con produzione e sottrazione diverse da zero, e non costanti.
Nei fenomeni di inquinamento da radon di un ambiente confinato (ma non isolato) normalmente P(t), Q(t), C(0) e quindi C(t) sono diversi da zero. Inoltre sovente P(t) e Q(t) e quindi C(t) dipendono dal tempo. Infatti i fenomeni di sorgente sono incostanti (si conoscono oscillazioni giornaliere e stagionali, dipendenti dalla pressione atmosferica, dall’umidità relativa, dalla temperatura esterna, dal tempo atmosferico, dalle condizioni fisico-chimiche del suolo e da altri fattori secondari); i fenomeni di “removal” (solo ventilazione per un gas) sono anch’essi estremamente variabili sia per le caratteristiche fisiche dell’ambiente confinato, che per i fattori atmosferici, ed anche per le abitudini di vita degli abitanti dell’edificio ove è collocato l’ambiente. L’unico parametro che non dipende dal tempo è la costante di decadimento radioattivo.
Per questo l’andamento del grafico del radon rilevato in un luogo confinato, anche dopo una fase di assestamento iniziale delle condizioni al contorno, non raggiunge praticamente mai una condizione di equilibrio. Ovviamente, per la complessità delle grandezze di sorgente e sottrazione non è facile esprimere analiticamente la situazione. La si può però rilevare a livello strumentale. Esemplificando la possiamo qui illustrare con l’andamento seguente :
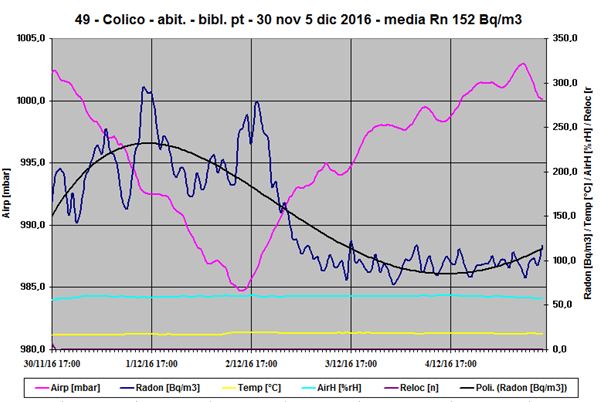
Come già fatto in precedenza, nel grafico, la grandezza CRn(t) è sostituita dalla ARn(t), ad essa proporzionale, meglio misurabile e di maggior interesse. Sono tracciati anche i grafici delle grandezze ambientali, utili appunto per indagarne le correlazioni con il radon.
Caso 5 – Radionuclide con produzione e coefficiente totale di sottrazione costanti, insieme alla sua progenie.
Veniamo adesso al caso dell’andamento temporale del Rn-222 con la sua progenie, in un locale confinato non isolato. Il coefficiente totale di sottrazione è diverso da zero, ma costante e quindi λtot = λRn+ λrem = costante. Inoltre ipotizziamo che λrem = 0. La concentrazione del radon, per quanto detto e per causa di una produzione costante, eventualmente dopo una fase iniziale (vedi caso 2), è quindi costante. La concentrazione della progenie, ipotizzata inizialmente pari a zero, varia nel tempo fino a raggiungere un equilibrio dopo circa sette T1/2. Studiamo prima la concentrazione di radon e poi quella dei figli.
Esaminiamo il Rn-222
Si parte dall’andamento della concentrazione nell’ambiente confinato non isolato di un radionuclide tipico, CA(t) [Nucl./m3], già vista nel caso 2, con sorgente dall’esterno P = F [Nucl./(m3sec)] e coefficiente totale di sottrazione λtot [sec-1], entrambe costanti.
CA(t) = CA(0) exp (- λtot*t) + F/λtot ( 1 – exp (- λtot*t) )
Come scritto sopra adesso abbiamo quindi:
A = Rn-222; λtot = λRn
Quindi Q [Nucl./(m3sec)] è dovuta al solo decadimento radioattivo (λRn) [sec-1]: Q = QRn = λRn*CRn
Dunque:
CRn(t) = CRn(0) exp (- λRn*t) + F/λRn (1 – exp (- λRn*t) )
Ricordando il valore della costante di decadimento del Rn-222, facciamo un’assunzione numerica per F molto più piccola di quella dei casi precedenti:
F = 3,7264[Nucl./(m3sec)]; λRn = 2,0982E-06 [sec-1]
per cui:
CRn(t) = CRn(0) exp (- λRn*t) + 1,776E+06 (1 – exp (- λRn*t) )
Dove per t >> 0:
CRn(∞) = 1,776E+06 [Nucl./m3]
Per semplicità possiamo assumere infine anche che:
CRn(0) = CRn(∞)
(Senza questa ipotesi CRn(t) varierebbe nel tempo passsando dal primo valore al secondo similmente al caso 2).
Si ha pertanto:
CRn(t) = 1,776E+06 [Nucl./m3] con F = 3,7264 [Nucl./(m3sec)]
Che corrispondono ad un’attività:
ARn(t) = ARn(0) = ARn(∞) = 3,7264 [Bq/m3]
Volendo normalizzare la concentrazione sulla produzione F
CRn(t) / F = (CRn(0) / F) exp (- λRn*t) + 1 / λRn (1 – exp (- λRn*t) )
CRn(t) = CRn(0) exp (- λRn*t) + 4,7659E+05 (1 – exp (- λRn*t) )
Allorché sarà raggiunto l’equilibrio secolare (cioè per t >> 0) si ha:
CRn(0) = CRn(∞) = 4,7659E+05 [Nucl./m3]
E quindi anche la concentrazione specifica normalizzata su F è costante:
CRn(t) = 4,7659E+05 [Nucl./m3]
Da cui si può passare ad un’attività specifica normalizzata su F:
ARn(t) = ARn(0) = ARn(∞) = 1 [Bq/m3]
Esaminiamo il Po-218
Torniamo alla equazione del caso 2, ma con P = K [Nucl./(m3sec)] = costante del caso 1:
CA(t) = CA(0) exp (- λtot*t) + K/λtot (1 – exp (- λtot*t) ) [Nucl./m3]
La sorgente P = K per il Po-218 è la trasmutazione del Rn-222 la cui concentrazione CRn è infatti costante. Anche il coefficiente totale di sottrazione λtot del Po-218 è costante e dovuto al solo decadimento radioattivo (λtot = λPo). Quindi si ha:
CPo(t) = CPo(0) exp (- λPo*t) + K/λPo (1 – exp (- λPo*t) ) [Nucl./m3]
Per ipotesi CPo(0) = 0 e K = λRn*CRn(t) = 3,7264 [Nucl./m3sec], quindi:
CPo(t) = CRn(t)*λRn/λPo (1 – exp (- λPo*t) ) [Nucl./m3]
Inserendo i dati:
CPo(t) = 1000 (1 – exp (- λPo*t) ) [Nucl./m3]
Per t >> 0 si avrà CPo(∞) = 1000 [Nucl./m3].
Il rapporto tra CRn(t) = 1,776E+06 [Nucl./m3] e CPo(∞) = 1000 [Nucl./m3] è pari a 1776 che è poi anche il rapporto tra le costanti di decadimento dei due radionuclidi Po-218 e Rn-222.
Passando dal numero di nuclidi per m3 C(t) alle attività specifiche A(t) si ha:
APo(t) = 3,7264 (1 – exp (- λPo*t) ) [Bq/m3]
Per t >> 0 si avrà un’attività APo(∞) di 3,7264 [Bq/m3], ovviamente uguale a quella del radon; il rapporto tra i due valori stavolta è pari a 1.
Volendo normalizzare l’attività specifica su ARn (t) si ha:
APo(t) = (1 – exp (- λPo*t) ) [Bq/m3]
Esaminiamo il Pb-214, il Bi-214, il Po-214 e il Pb-210
La sorgente P(t) per il Pb-214 è dovuta alla trasmutazione del genitore Po-218 la cui concentrazione CPo (t) è quella sopraesaminata. Il coefficiente totale di sottrazione λtot del Pb-214 è costante e dovuto al solo decadimento radioattivo (λtot = λPb).
Ugualmente si può dire per il Bi-214, il Po-214 e il Pb-210 facendo riferimento ai loro nuclidi genitori.
Non riportiamo le espressioni analitiche degli andamenti dei radionuclidi per semplicità. Alleghiamo però qui sotto due grafici complessivi che li illustrano.
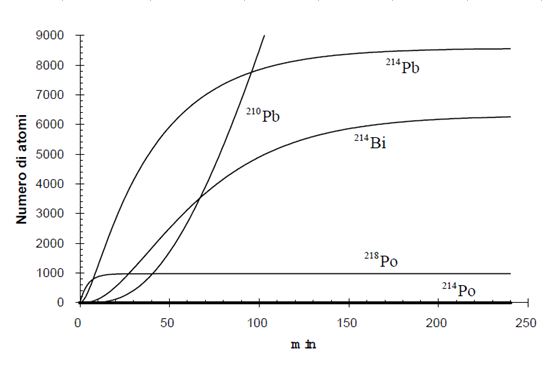
CRn = cost = 1,776E+06 [Nucl./m3] (valore fuori campo)
Il grafico di fig.7 mostra gli andamenti delle concentrazioni specifiche C(t) in [Nucl./m3] dei radionuclidi figli del Rn-222 fino al Pb-210, nell’assunzione esemplificativa che si abbia una sorgente esterna F = 3,7264 [Nucl./(m3 sec)] e quindi che la concentrazione specifica del radon CRn(t) (costante) sia pari a 1,776E+06 [Nucl./m3], non indicata perché fuori campo.
Le concentrazioni dei figli a breve vita (inizialmente pari a zero) raggiungono l’equilibrio dopo 3-4 ore (singolarmente dopo circa 7 tempi di dimezzamento). I valori di equilibrio dei radionuclidi stanno alla concentrazione costante del radon come le rispettive costanti di decadimento. Il valore di equilibrio della concentrazione del Po-214 è praticamente zero. Infatti il numero dei radionuclidi per m3 all’equilibrio è tanto minore quanto più grande è la loro attività (costante di decadimento). Il grafico del Pb-210 è invece tipico di un nuclide quasi stabile, data la sua piccola costante di decadimento che è più di 1000 volte minore di quella del radon; la sua concentrazione specifica raggiungerà l’equilibrio, dopo oltre 150 anni, a circa 3,76 E+09 [Nucl./m3], ovviamente anch’esso fuori campo dal grafico.

Questo secondo grafico illustra invece gli andamenti delle attività specifiche dei radionuclidi figli del Rn-222. Sono mostrate più esattamente le attività specifiche A(t) normalizzate su quella del radon (costante). L’attività specifica relativa del Pb-210 non è mostrata in quanto è praticamente nulla, per il valore molto piccolo della sua costante di decadimento; comincerebbe a notarsi nel grafico dopo una decina di anni e raggiungerebbe l’equilibrio, cioè vicino a 1, dopo 150-200 anni. L’equilibrio delle attività dei radionuclidi è raggiunto dopo 20′ per il Po-218 e per tutti gli altri poco dopo le tre ore. I grafici del Bi-214 e del Po-214 coincidono per la piccolissima vita media di quest’ultimo.
Caso 6 – Radionuclide genitore con produzione nulla, concentrazione iniziale e coefficiente totale di sottrazione diverse da zero, insieme alla sua progenie
E’ il fenomeno di un radionuclide che attiva, in un ambiente confinato, una catena di decadimenti fino ad arrivare ad un nuclide stabile. La concentrazione iniziale del primo radionuclide è diversa da zero, mentre quella iniziale dei nuclidi della progenie è nulla. Il coefficiente totale di sottrazione di ciascun radionuclide coincide con la sua costante di decadimento ed è quindi costante; l’ultimo nuclide (quasi stabile nel nostro caso) non ha praticamente sottrazione.
Ipotizziamo, per esempio, la concentrazione al tempo zero del Rn-222 CRn(0) = 3,407E+09 [Nucl./m3]. La corrispondente attività sappiamo che è allora ARn(0) = 7149 [Bq/m3].
Dalla letteratura (Modern Nuclear Chemistry – Loveland Morrissay Seaborg – 2006 – John Wiley & Sons, Inc., Publication) si ricava che le equazioni della concentrazione di ciascun radionuclide applicabili nelle condizioni sopra dette sono quelle di Bateman . L’equazione tipo per il radionuclide “n” è:
Cn(t) = ε1 (exp (- λ1 t)) + ε2 (exp (- λ2 t)) + ε3 (exp (- λ3 t)) + ….. + εn (exp (- λn t)) [Nucl./m3]
dove:
ε1 = C1(0) λ1 λ2 λ3,…., λn-1 / (λ2-λ1)(λ3- λ1),….,(λn-λ1)
ε2 = C1(0) λ1 λ2 λ3,…., λn-1 / (λ1-λ2)(λ3- λ2),….,(λn-λ2)
ε3 = C1(0) λ1 λ2 λ3,…., λn-1 / (λ1-λ3)(λ2- λ3),….,(λn-λ3)
εn = C1(0) λ1 λ2 λ3,…., λn-1 / (λ1-λn)(λ2- λn),….,(λn-1-λn)
Esaminiamo il Rn-222.
La sorgente P(t) è nulla, mentre la sottrazione Q(t) è dovuta al decadimento radioattivo del RN-222 stesso. Si applicano le note equazioni per la concentrazione e l’attività del radon (vedi il precedente caso 3):
CRn(t) = CRn(0) (exp (- λRn t)) [Nucl./m3] ARn(t) = ARn(0) (exp (- λRn t)) [Bq/m3]
Inseriamo i dati numerici ipotizzati:
CRn(t) = 3,407E+09 (exp (- λRn t)) [Nucl./m3] ARn(t) = 7149 (exp (- λRn t)) [Bq/m3]
Volendo normalizzare l’attività specifica su ARn (0) =7149 [Bq/m3] si ha:
ARn(t) = (exp (- λRn t)) [Bq/m3]
Esaminiamo il Po-218.
La sorgente P(t) è il decadimento del Rn-222 (P = λRn*CRn). Mentre Q(t) è dovuta al decadimento radioattivo del Po-218 (λPo*CPo). Quindi utilizzando le equazioni di Bateman con n=2 si ha:
CPo(t) = λRn / (λPo – λRn) CRn(0) (exp (- λRn*t) – exp (- λPo*t )) [Nucl./m3]
APo(t) = λPo / (λPo – λRn) ARn(0) (exp (- λRn*t) – exp (- λPo*t )) [Bq/m3]
Inseriamo i dati numerici delle costanti di decadimento e dei valori al tempo zero del radon:
CPo(t) = 5,634E-04 * 3,407E+09 (exp (- λRn*t) – exp (- λPo*t )) [Nucl./m3]
APo(t) = 1,00056 * 7149 (exp (- λRn*t) – exp (- λPo*t )) [Bq/m3]
CPo(t) = 1919,5E+03 (exp (- λRn*t) – exp (- λPo*t )) [Nucl./m3]
APo(t) = 7153 (exp (- λRn*t) – exp (- λPo*t )) [Bq/m3]
Volendo normalizzare l’attività specifica del Po-218 su ARn (0) = 7149 [Bq/m3] si ha:
APo(t) = 1,00056 (exp (- λRn*t) – exp (- λPo*t )) [Bq/m3]
Esaminiamo adesso il Pb-214.
La sorgente P(t) è il decadimento del Po-218 (P = λPo*CPO). Mentre Q(t) è dovuta al decadimento radioattivo del Pb-214 (λPb*CPb).
Utilizzando l’equazione di Bateman soprascritta con n=3 si ha:
CPb(t) = CRn(0){*[λRn λPo / ((λPo – λRn) (λPb – λRn)) ]*exp (- λRn*t) + [λRn λPo / ((λRn – λPo) (λPb – λPo)) ]*exp (- λPo*t) + [λRn λPo / ((λRn – λPb) (λPo – λPb)) ]*exp (- λPb*t)}
Passando dal numero di nuclidi per metro cubo C(t) alle attività specifiche A(t) si ha:
APb(t) = ARn(0) λPb / λRn {*[λRn λPo / ((λPo – λRn) (λPb – λRn)) ]*exp (- λRn*t) + [λRn λPo / ((λRn – λPo) (λPb – λPo)) ]*exp (- λPo*t) + [λRn λPo / ((λRn – λPb) (λPo – λPb)) ]*exp (- λPb*t)}
Inseriamo i dati numerici:
APb(t) = 7149 * 205,4 {*[7,819E-09/ ((3,724E-03) (4,290E-04)) ]*exp (- λRn*t) + [7,819E-09/ ((-3,724E-03) (-3,296E-03)) ]*exp (- λPo*t) + [7,819E-09/ ((-4,290E-04) (3,296E-03)) ]*exp (- λPb*t)}
APb(t) = 7182,9*exp (- λRn*t) + 935,4*exp (- λPo*t) – 8118*exp (- λPb*t)} [Bq/m3]
Tornando dalla attività alla concentrazione di radionuclidi si ha, dividendo per λPb = 4,311E-04:
CPb(t) = 1,666E+07*exp (- λRn*t) + 2,1698E+06*exp (- λPo*t) – 1,883E+07*exp (- λPb*t)} [Nucl./m3]
Volendo invece normalizzare l’attività specifica del Pb-214 su ARn (0) = 7149 [Bq/m3] si ha:
APb(t) = 1,0047*exp (- λRn*t) + 0,13084*exp (- λPo*t) – 1,1355*exp (- λPb*t)} [Bq/m3]
Esaminiamo adesso il Bi-214.
La sorgente P(t) è il decadimento del Pb-214 (P = λPb*CPb). Mentre Q(t) è dovuta al decadimento radioattivo del Bi-214 (λBi*CBi).
Utilizziamo l’equazione di Bateman con n=4.
CBi(t) = CRn(0){[λRn λPo λPb / ((λPo – λRn) (λPb – λRn) (λBi – λRn ) ]*exp (- λRn*t) + [λRn λPo λPb / ((λRn – λPo) (λPb – λPo) (λBi – λPo))] *exp (- λPo*t) + [λRn λPo λPb / ((λRn – λPb) (λPo – λPb) (λBi – λPb)) ]*exp (- λPb*t) + [λRn λPo λPb / ((λRn – λBi) (λPo – λBi) (λPb – λBi))]*exp (- λBi*t)}
Passando dal numero di nuclidi C alle attività A si ha:
ABi(t) = ARn(0) λBi / λRn{[λRn λPo λPb / ((λPo – λRn) (λPb – λRn) (λBi – λRn ))]*exp (- λRn*t) + [λRn λPo λPb / ((λRn – λPo) (λPb – λPo) (λBi – λPo))] *exp (- λPo*t) + [λRn λPo λPb / ((λRn – λPb) (λPo – λPb) (λBi – λPb)) ]*exp (- λPb*t) + [λRn λPo λPb / ((λRn – λBi) (λPo – λBi) (λPb – λBi))]*exp (- λBi*t)}
Inseriamo i dati numerici:
ABi(t) = 7149* 276,7{[3,371E-12 / (3,724E-3 * 4,290E-4 * 5,784E-4) ]*exp (- λRn*t) + [3,371E-12 / ((-3,724E-03)* (-3,296E-3)* (-3,146E-03))] *exp (- λPo*t) + [3,371E-12 / ((-4,290E-04)* (3,296E-03)*(1,494E-4)) ]*exp (- λPb*t) + [3,371E-12 / ((-5,784E-04)*(3,146E-03)*(-1,494E-04))]*exp (- λBi*t)}
ABi(t) = 7216*exp (- λRn*t) -172,7 *exp (- λPo*t) -31570*exp (- λPb*t) + 24530*exp (- λBi*t)} [Bq/m3]
Tornando dalla attività alla concentrazione di radionuclidi si ha, dividendo per λBi = 5,805E-04:
CBi(t) = 1,243E+07*exp (- λRn*t) – 2,1998E+05 *exp (- λPo*t) – 5,4384E+07*exp (- λPb*t) + 4,2257E+07*exp (- λBi*t)} [Nucl./m3]
Volendo invece normalizzare l’attività specifica del Bi-214 su ARn (0) = 7149 [Bq/m3] si ha:
ABi(t) = 1,0094*exp (- λRn*t) – 0,02416 *exp (- λPo*t) – 4,416*exp (- λPb*t) + 3,431*exp (- λBi*t)} [Bq/m3]
Esaminiamo adesso il Po-214.
La sorgente P(t) è il decadimento del Bi-214 (P = λBi*CBi). Mentre Q(t) è dovuta al decadimento radioattivo del Po-214 (λPo214*CPo214).
Utilizziamo l’equazione di Bateman con n=5.
CPo214(t) = CRn(0){[λRn λPo λPb λBi / ((λPo – λRn) (λPb – λRn) (λBi – λRn ) (λPo214 – λRn))]*exp (- λRn*t) + [λRn λPo λPb λBi / ((λRn – λPo) (λPb – λPo) (λBi – λPo) ( λPo214 – λPo))]*exp (- λPo*t) + [λRn λPo λPb λBi / ((λRn – λPb) (λPo – λPb) (λBi – λPb) (λPo214 – λPb))]*exp (- λPb*t) + [λRn λPo λPb λBi / ((λRn – λBi) (λPo – λBi) (λPb – λBi) (λPo214 – λBi))]*exp (- λBi*t) + [λRn λPo λPb λBi / ((λRn – λPo214) (λPo – λPo214) (λPb – λPo214) (λBi – λPo214))]*exp (-λPo214*t)}
Passando dalla concentrazione di nuclidi C alla attività A si ha:
APo214(t) = ARn(0) (λPo214 / λRn) {[λRn λPo λPb λBi / ((λPo – λRn) (λPb – λRn) (λBi – λRn ) (λPo214 – λRn))]*exp (- λRn*t) + [λRn λPo λPb λBi / ((λRn – λPo) (λPb – λPo) (λBi – λPo) ( λPo214 – λPo))]*exp (- λPo*t) + [λRn λPo λPb λBi / ((λRn – λPb) (λPo – λPb) (λBi – λPb) (λPo214 – λPb))]*exp (- λPb*t) + [λRn λPo λPb λBi / ((λRn – λBi) (λPo – λBi) (λPb – λBi) (λPo214 – λBi))]*exp (- λBi*t) + [λRn λPo λPb λBi / ((λRn – λPo214) (λPo – λPo214) (λPb – λPo214) (λBi – λPo214))]*exp (-λPo214*t)}
Inseriamo i dati numerici:
APo214(t) = 7149* 2,011E+09{[1,957E-15 / ((3,724E-03) (4,290E-04) (5,784E-04) (4,219E+03))]*exp (- λRn*t) + [1,957E-15 / ((-3,724E-03) (-3,296E-03) (-3,146E-03) (4,219E+03))]*exp (- λPo*t) + [1,957E-15 / ((-4,290E-04) (3,296E-03) (1,494E-04) (4,219E+03))]*exp (- λPb*t) + [1,957E-15 / ((-5,784E-04) (3,146E-03) (-1,494E-04) (4,219E+03))]*exp (- λBi*t) + [1,957E-15 / ((-4,219E+03) (-4,219E+03) (-4,219E+03) (-4,219E+03))]*exp (-λPo214*t)}
APo214(t) = 7216*exp (- λRn*t) – 172,7*exp (- λPo*t) – 31570*exp (- λPb*t) + 24530*exp (- λBi*t) + 8,881E-17*exp (-λPo214*t) [Bq/m3]
Tornando dalla attività alla concentrazione di radionuclidi si ha, dividendo per λPo214 = 4,219E+03:
CPo214(t) = 1,710*exp (- λRn*t) – 4,0934E-02*exp (- λPo*t) – 7,4828*exp (- λPb*t) + 5,8142*exp (- λBi*t) + 2,1050E-20*exp (-λPo214*t) [Nucl./m3]
Volendo invece normalizzare l’attività specifica del Po-214 su ARn (0) si divide per 7149 [Bq/m3] e si ha:
APo214(t) = 1,0094*exp (- λRn*t) – 0,02416*exp (- λPo*t) – 4,416*exp (- λPb*t) + 3,431*exp (- λBi*t) + 1,2423E-20*exp (-λPo214*t) [Bq/m3]
E’ interessante notare come l’equazione dell’attività del Po-214 sia praticamente identica a quella del Bi-214, come prevedibile tenendo conto della piccolissima vita media del Po-214. E’ come, per questo, se il Bi-214 decadesse direttamente nel Pb-210 e il Po-214 non esistesse. Il Pb-210 ha una lunga vita media, circa 32 anni, e quindi lo potremo considerare quasi un nuclide stabile.
Esaminiamo adesso il Pb-210.
La sorgente P(t) è il decadimento del Po-214 (P = λPo214*CPo214). Mentre Q(t) è dovuta alla piccola costante di decadimento λPb210 (9,90E-10).
Utilizzando l’equazione di Bateman soprascritta con n=6 si ha:
CPb210(t) = CRn(0){[λRn λPo λPb λBi λPo214 / ((λPo – λRn) (λPb – λRn) (λBi – λRn ) (λPo214 – λRn) (λPb210 – λRn))]*exp (- λRn*t) + [λRn λPo λPb λBi λPo214 / ((λRn – λPo) (λPb – λPo) (λBi – λPo) ( λPo214 – λPo) (λPb210 – λPo))]*exp (- λPo*t) + [λRn λPo λPb λBi λPo214 / ((λRn – λPb) (λPo – λPb) (λBi – λPb) (λPo214 – λPb) (λPb210 – λPb))]*exp (- λPb*t) + [λRn λPo λPb λBi λPo214 / ((λRn – λBi) (λPo – λBi) (λPb – λBi) (λPo214 – λBi) (λPb210 – λBi))]*exp (- λBi*t) + [λRn λPo λPb λBi λPo214 / ((λRn – λPo214) (λPo – λPo214) (λPb – λPo214) (λBi – λPo214) (λPb210 – λPo214))]*exp (-λPo214*t) + [λRn λPo λPb λBi λPo214 / ((λRn – λPb210) (λPo – λPb210) (λPb – λPb210) (λBi – λPb210) (λPo214 – λPb210))]*exp (-λPb210*t)}
Inseriamo i dati numerici:
CPb210(t) = CRn(0) {[8,173E-21 / ((3,724E-03) (4,290E-04) (2,767E+02) (4,219E+03) (9,900E-10 – 2,0982E-06))]*exp (- λRn*t) + [8,173E-21 / ((-3,724E-03) (-3,296E-03) (-3,146E-03) (4,219E+03) (9,900E-10 – 3,73E-03))]*exp (- λPo*t) + [8,173E-21 / ((- 4,290E-04) (3,296E-03) (1,494E-04) (4,219E+03) (9,900E-10 – 4,31E-04))]*exp (- λPb*t) + [8,173E-21 / ((-5,784E-04) (3,146E-03) (-1,494E-04) (4,219E+03) (9,900E-10 -5,81E-04))]*exp (- λBi*t) + [8,173E-21 / ((-4,219E+03) (-4,219E+03) (-4,219E+03) (-4,219E+03) (9,900E-10 – 4,22E+03))]*exp (-λPo214*t) + [8,173E-21 / ((2,0982E-06 – 9,900E-10)(3,7266E-03 – 9,900E-10)(4,31E-04 – 9,900E-10)(5,81E-04 – 9,900E-10)(4,22E+03 – 9,900E-10))]*exp(-λPb210*t)}
CPb210(t) = CRn(0) {-2,090E-15*exp (- λRn*t) + 1,345E-14*exp (- λPo*t) -2,128E-11*exp (- λPb*t) -1,226E-11*exp (- λBi*t) -6,113E-39*exp (-λPo214*t) + 9,896E-10*exp(-λPb210*t)}
Passando dalla concentrazione di nuclidi C all’attività A si ha:
APb210(t) = ARn(0) (λPb210/λRn) {-2,090E-15*exp (- λRn*t) + 1,345E-14*exp (- λPo*t) -2,128E-11*exp (- λPb*t) -1,226E-11*exp (- λBi*t) -6,113E-39*exp (-λPo214*t) + 9,896E-10*exp(-λPb210*t)} [Bq/m3]
APb210(t) = ARn(0) 4,719E-04 {-2,090E-15*exp (- λRn*t) + 1,345E-14*exp (- λPo*t) -2,128E-11*exp (- λPb*t) -1,226E-11*exp (- λBi*t) -6,113E-39*exp (-λPo214*t) + 9,896E-10*exp(-λPb210*t)} [Bq/m3]
APb210(t) = ARn(0) {-9,863E-16*exp (- λRn*t) + 6,347E-18*exp (- λPo*t) -1,004E-14*exp (- λPb*t) -5,785E-15*exp (- λBi*t) -2,885E-42*exp (-λPo214*t) + 4,667E-13*exp(-λPb210*t)} [Bq/m3]
Tornando dalla attività alla concentrazione di radionuclidi si ha, dividendo per λPb210 = 9,901E-10:
CPb210(t) = -7,122E-03*exp (- λRn*t) + 4,583E-05*exp (- λPo*t) -7,249E-02*exp (- λPb*t) -4,177E-02*exp (- λBi*t) -2,083E-29*exp (-λPo214*t) + 3,3698*exp(-λPb210*t) [Nucl./m3]
Volendo invece normalizzare l’attività specifica del Pb-210 su ARn (0) = 7149 [Bq/m3] si ha:
APb210(t) = -9,863E-16*exp (- λRn*t) + 6,347E-18*exp (- λPo*t) -1,004E-14*exp (- λPb*t) -5,785E-15*exp (- λBi*t) -2,885E-42*exp (-λPo214*t) + 4,667E-13*exp(-λPb210*t) [Bq/m3]
Calcoliamo le tabelle e costruiamo i grafici delle concentrazioni specifiche C(t) ottenute analiticamente:
Tabella dei valori della concentrazione specifica del Rn-222 nel tempo
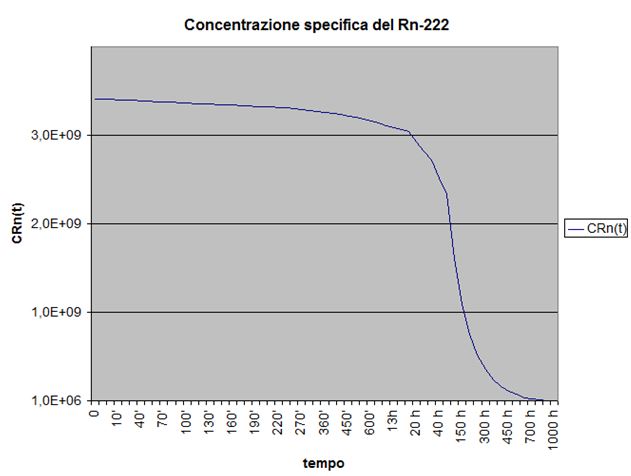
Dalla tabella e dal relativo grafico di fig. 9 si vede che il valore della concentrazione specifica del Rn-222 cala ad un centesimo del valore iniziale dopo circa 600 ore (7 tempi di dimezzamento) e ad un millesimo dopo circa 900 ore (10 tempi di dimezzamento).
Tabella dei valori della concentrazione specifica del Po-218, Pb-214 e del Bi-214 nel tempo
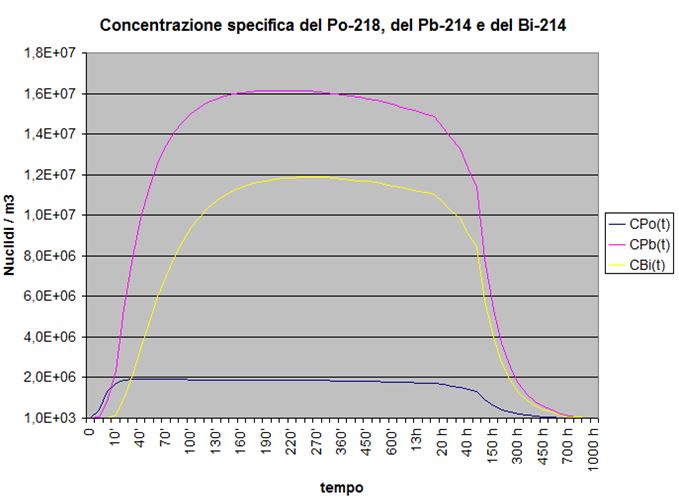
Fig. 10
Da notare che i valori massimi della concentrazione specifica si raggiungono dopo circa 30′ per il Po-218 e dopo circa 4 ore per gli altri due radionuclidi.
Tabella dei valori della concentrazione specifica del Po-214 e del Pb-210 nel tempo
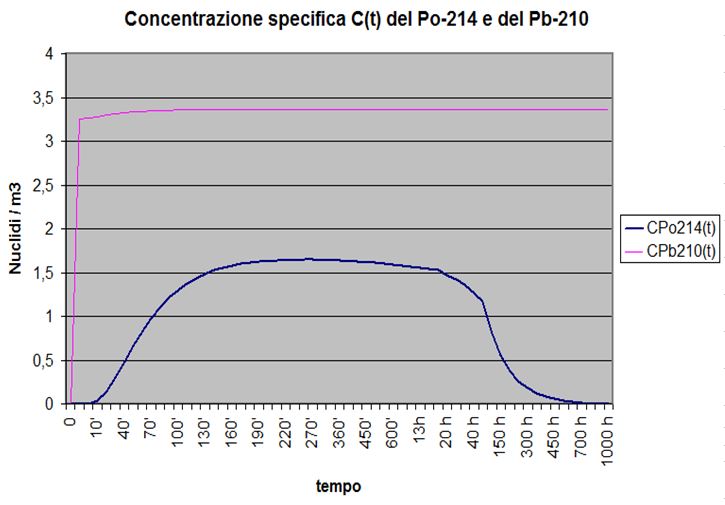
Fig. 11
Il grafico del Pb-210 scenderà a valori prossimi allo zero fuori campo, dopo circa 1,3E+06 ore (circa 150 anni).
Adesso calcoliamo la tabella e costruiamo il grafico delle attività specifiche normalizzate A(t):
Tabella dei valori delle attività specifiche normalizzate di tutti i radionuclidi nel tempo
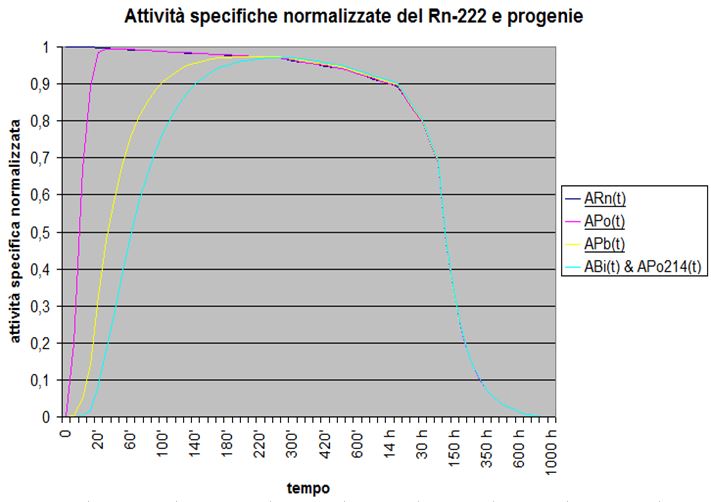
Fig. 12
I valori della attività specifica normalizzata del Pb-210 non sono rilevabili nel grafico a causa della loro piccolezza (intorno a 1E-13). Analogamente il grafico dell’attività normalizzata del Rn-222 è sovrapposto, al di sopra dei 30′, a quello del Po-218 , per una differenza di pochi per mille.
Revisionato luglio 2023
